Jobs
On this page, you will find our opportunities for interns, PhD students, and post-doctoral researchers…
If none of the positions match your profile, feel free to contact our teams directly.
You can also find our internship opportunities on the Sorbonne University and ENS – PSL websites.
Some of our job openings for PhD candidates, postdocs, and IT positions are available on the CNRS website.
Post-doctoral positions – Experimental Continuous-Variable Gaussian & Non-Gaussian Quantum Resources
Postdoctoral positions are open at Laboratoire Kastler Brossel (LKB) in the Multimode Quantum Optics group to work on the implementation of continuous-variable platforms.
The Multimode Quantum Optics group at LKB has carried out leading research in the experimental generation of squeezed and continuous-variable entangled states for the implementation of quantum information protocols. The activities in this area range from the generation of large entangled networks multiplexed both in time and frequency [1,2,3], to the implementation and verification of non-Gaussian operations in all-optical setups [4,5] and the development of tailored CV quantum optical resources for light–matter interactions [6].
Continuous-variable encoding of quantum information allows for the deterministic generation of entangled networks, where multimode capabilities provide scalability of Gaussian quantum resources. Tailored non-Gaussian quantum operations can be implemented via heralded non-linear optical processes or through collective interactions with atomic systems.
Positions are available on several of these research topics. The experimental work will be carried out in collaboration with the in-house theoretical team, as well as with French and international consortia, including both theoretical and experimental groups, and industrial partners in the quantum sector. These collaborations will support the expansion of your scientific network and the establishment of new international partnerships.
List of current funded projects related to the proposed work:
EIC Pathfinder VeriQub (European Innovation Council): https://veriqub.eu
EIC Pathfinder PANDA (European Innovation Council): https://www.pasqal.com/fr/project-panda/
National Acceleration Strategy PEPR OQULUS:
https://www.pepr-quantique.fr/en/projet/oqulus/
[1] V. Roman-Rodriguez, D. Fainsin, G.L. Zanin, N. Treps, E. Diamanti, V. Parigi Multimode squeezed state for reconfigurable quantum networks at telecommunication wavelengths Physical Review Research 6 (4), 043113 (2024)
[2] T. Kouadou, F. Sansavini, M. Ansquer, J. Henaff, N. Treps, V. Parigi Spectrally shaped and pulse-by-pulse multiplexed multimode squeezed states of light APL Photonics 8 (2023)
[3] Y. Cai, J. Roslund, G. Ferrini, F. Arzani, X. Xu, C. Fabre, N. Treps Multimode entanglement in reconfigurable graph states using optical frequency combs Nature communications 8 (1), 15645 (2017)
[4] YS Ra, A Dufour, M Walschaers, C Jacquard, T Michel, C Fabre, N Treps Non-Gaussian quantum states of a multimode light fieldNature Physics 16 (2), 144-147 (2020)
[5] U. Chabaud, G. Roeland, M. Walschaers, F. Grosshans, V. Parigi, D. Markham, N. Treps Certification of non-Gaussian states with operational measurements PRX Quantum 2 (2), 020333 (2021)
[6] M. Moreno-Cardoner, D. Goncalves and D. E. Chang Quantum Nonlinear Optics Based on Two-Dimensional Rydberg Atom Arrays Phys. Rev. Lett. 127, 263602 (2021)
Environment
As a whole, the group has a tradition of working together with a diverse range of people from varied backgrounds. This diversity often leads to fruitful scientific input from different points of view, and it allows the group to explore new avenues. Furthermore, the moderate size of our group gives PhD students and postdocs the opportunity to discuss with PIs on a daily basis. This gives rise to a dynamical atmosphere with a lot of space for discussion.
Laboratoire Kastler Brossel is one of the main worldwide leaders in the field of fundamental physics of quantum systems, covering a number of subjects spanning from fundamental tests of quantum theory to applications. It has an internationally recognized expertise throughout its 65 years history, including three Nobel Prize winners. The multimode quantum optics team explore both fundamental science and applications in CV quantum information. Based in Sorbonne Université in the Pierre and Marie Curie Campus in the center of Paris, it is part of the Quantum Information Center (QICS) in Sorbonne, hosting both quantum physicists and computer scientists. It is also part of the Paris Centre for Quantum Technologies (PCQT), a research, training and innovation network involving 22 research laboratories in Paris Region, 35 start-ups and larger industry groups.
Practical information
Candidates must hold an internationally recognized PhD in a field related to experimental quantum physics. A good background and past research track record in experimental optics, and quantum physics is required.
Application procedure: Inquiries and applications (incl. a detailed CV and two names of potential referees) should be sent by email to Nicolas Treps (nicolas.treps@lkb.upmc.fr) and Valentina Parigi(valentina.parigi@lkb.upmc.fr).
Salary: Monthly net salary (after-tax) between 2300€ and 3000€, depending on experience
Application deadline: Preferentially apply before December 1st 2025
Starting date: flexible
Duration: up to 2 years (with possible renewal of 1 year)

Post-doctoral position: Architecture for photonic quantum computing
A postdoctoral position is open at Laboratoire Kastler Brossel to work on the theory of photonic quantum computing.
The project is focused on exploration of new photonic quantum computing architectures. Rapid progress in development of quantum computers, especially with enabling technologies, offers extended possibilities for new computational paradigms. Coming back to the core architecture, your role will involve identifying a novel path toward Fault-Tolerant Universal quantum computing with continuous variables. This requires investigations in transverse domains, from resource theory with non-gaussian states, breeding protocols, universal gates for quantum computing and error correcting strategies.
The multimode quantum optics group at LKB carried out leading research in the study of multimode Gaussian and non-Gaussian states of light, useful in quantum information protocol on a large scale. The group has a strong experimental focus, but is also engaged in purely theoretical activities aiming at developing quantum technologies in the continuous- variable framework. This project also fits within its technology transfer strategy.
In a nutshell,
Why apply?
You are at a core moment of your academic career where you would like to explore a large variety of subjects from quantum information theory to experiment with different hardware
You will benefit of an international team of researchers, expert in continuous variables quantum optics
It is an opportunity to build an extensive network of researchers, joining and building research consortia at national, european and world level.
Our specific view:
Photonic quantum computing with continuous variables
Close interplay between quantum information theory and quantum optics experiments
Exploring the entanglement properties of non-Gaussian quantum states of light
Environment
As a whole, the group has a tradition of working together with a diverse range of people from varied backgrounds. This diversity often leads to fruitful scientific input from different points of view, and it allows the group to explore new avenues. Furthermore, the moderate size of our group gives PhD students and postdocs the opportunity to discuss with PIs on a daily basis. This gives rise to a dynamical atmosphere with a lot of space for discussion.
Your work fits in the OQULUS project (part of the quantum strategy within the framework France 2030). This framework provides support to enlarge your scientific network and establish new international collaborations as well as enables possibility for technology transfer.
Practical information
Candidates must hold an internationally recognized PhD in a field related to theoretical quantum physics. A good background and past research track record in either theoretical quantum optics or quantum information theory is required.
Application procedure
Inquiries and applications should be sent by email to Mattia Walschaers (mattia.walschaers@lkb.upmc.fr). Applications should include a detailed CV and two names of potential referees.
Salary: Monthly net salary (after-tax) between 2300€ and 3000€, depending on experience
Application deadline: Preferentially apply before December 1st 2025.
Starting date: flexible
Duration: 2 years

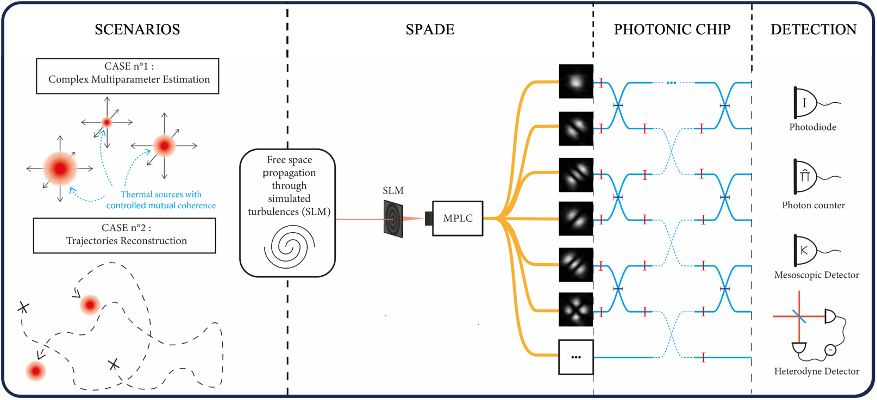
Post-doctoral position Modal approach to (quantum) multi-parameter estimation in optics
The Rayleigh criterion, once considered a fundamental limit in imaging, has been surpassed by quantum-inspired metrology techniques like Spatial Mode demultiplexing (SPADE) [1]. This post-doctoral project aims to extend SPADE’s capabilities to multi-parameter estimation, low-flux detection, and dynamic source tracking. The post-doc will work on/supervise an experimental setup aimed at multi-parameter estimation from individual incoherent optical sources [2] using a Multi-Plane Light Convertor [3]. She/He will also participate in the theoretical effort in deriving optimal quantum bounds [4] and optimal estimators [5].
The multimode quantum optics group pioneered the modal approach to quantum metrology [6] and obtained unparalleled sensitivity in source separation estimation [2] using a unique technology invented in the group [3]. The group has a strong experimental focus, but is also engaged in purely theoretical activities aiming at developing quantum optics in the continuous variable (CV) framework.
In a nutshell
Why to apply:
-you are passionate about fundamental quantum science and/or technological applications
-you will benefit from an international team of researchers who are experts in Continuous Variable quantum optics and metrology (theory and experiment)
– you will be in a group at the core of many national and international research networks
Our specific view:
– Experiments and theory should go together to implement practical parameter estimation at the quantum limit
– Modal approach to quantum metrology allows both for quantum limited parameter estimation and to derive theoretical bounds closely related
Environment
As a whole, the group has a tradition of working together with a diverse range of people from varied backgrounds. This diversity often leads to fruitful scientific input from different points of view, and it allows the group to explore new avenues. Furthermore, the moderate size of our group gives PhD students and postdocs the opportunity to discuss with PIs on a daily basis. This fosters a dynamic atmosphere with a lot of space for discussion.
Your work will be supported by the CEA-Audace project Lumiere, which aims to provide support and build collaborations. Notably, the project will enable you to gain access to groundbreaking multi-photon detectors with very high sensitivity and fast response time, promising significant advancements in metrology and tracking applications.
The project is inherently interdisciplinary, bridging quantum optics with fields such as signal processing, machine learning, and advanced instrumentation. It also benefits from strong collaborations with national and international teams, ensuring frequent exchanges of ideas and expertise.
Practical information
Candidates must hold an internationally recognized PhD in a field related to experimental quantum physics. A good background and past research track record in experimental optics, and quantum physics is required.
Application procedure: Inquiries and applications should be sent by email to Nicolas Treps(nicolas.treps@lkb.upmc.fr). Applications should include a detailed CV and two names of potential referees
Salary: Monthly net salary (after-tax) between 2200€ and 2900€, depending on experience
Application deadline: Preferentially apply before 16 May 2025
Starting date: flexible
Duration: 2 years (with possible renewal of 1 year)
References
[1] Tsang, M., Nair, R., & Lu, X. M. (2016). Quantum theory of superresolution for two incoherent optical point sources. Physical Review X, 6(3), 031033.
[2] Rouvière, C., Barral, D., Grateau, A., Karuseichyk, I., Sorelli, G., Walschaers, M., & Treps, N. (2024). Ultra-sensitive separation estimation of optical sources. Optica, 11(2), 166-170.
[3] G. Labroille, BertrDenolle, P. Jian, P. Genevaux, N. Treps, and J.-F. Morizur, Efficient and mode selective spatial mode multiplexer based on multi-plane light conversion, Opt Express 22, 15599 (2014).
[4] Gessner, M., Treps, N., & Fabre, C. (2023). Estimation of a parameter encoded in the modal structure of a light beam: a quantum theory. Optica, 10(8), 996-999.
[5] G. Sorelli, M. Gessner, M. Walschaers, and N. Treps, Optimal Observables and Estimators for Practical Superresolution Imaging, Phys. Rev. Lett. 127, 123604 (2021).
[6] C. Fabre and N. Treps, Modes and States in Quantum Optics, Rev. Mod. Phys. 92, 035005 (2020).