Wigner Negativity
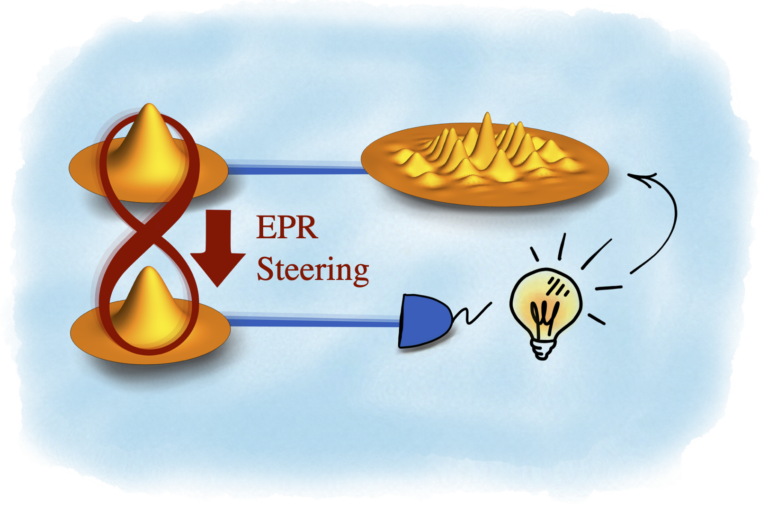
The Wigner function is a representation of quantum states and quantum observables on phase space. As a representation of a quantum state it has the unique property of correctly representing all the measurement statistics of field quadratures as its marginals. However, even though it reproduces all the measureable quadrature statistics, the function itself is generally not a probability distribution. In particular, Wigner functions can sometimes be negative in certain regions of phase space. This negativity is known to be a continuous-variable manifestation of contextuality, and it is also known to be a necessary resource for reaching a quantum computational advantage. In our research, we explore various aspects of this Wigner negativity. First, we try to undersatnd how Wigner negativity can be generated in experiments. Here we have for example shown that a measurement-based generation of Wigner negativity starting form a Gaussian state requires quantum steering. Reciprocally, we also inverstigate the role of Wigner negativity to generate quantum correlations. Finally, we better quantify its importance in in quantum computing and quantum metrology.
Techniques used: Phase space representations, Moyal calculus, stellar representation, probability theory, functional analysis …
Non-Gaussian quantum correlations
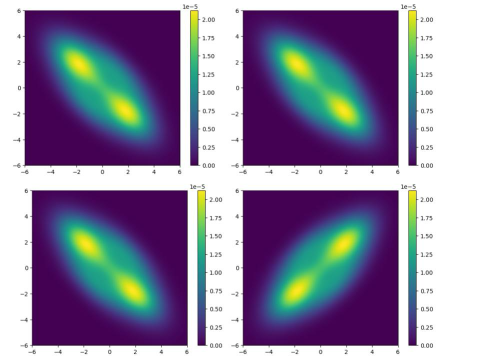
In continuous variable systems, quantum correlations have been studied in great detail for Gaussian states. Many of the Gaussian techniques can be applied to also detect certain instances of quantum correlations in non-Gaussian states. However, non-Gaussian states provide much more structure than what can be captured in a covariance matrix. In our group, we try to understand quantum correlations in non-Gaussian states exactly where Gaussian techniques fail. This notably leads us to investigate quantum states with entanglement that survives in every mode basis or under every Gaussian unitary transformations.
Techniques used: (Quantum) Fisher information, Wigner functions, stellar representation, convex analysis, neural networks, …
Quantum computational advantages
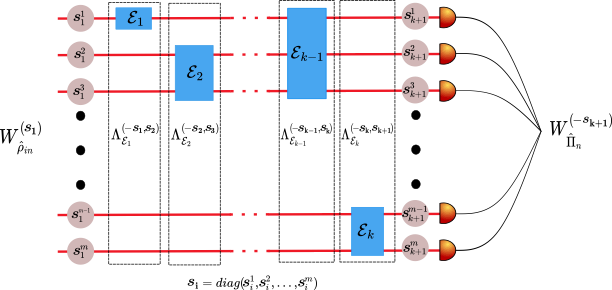
In some important work, we showed that any boson sampling setup can be strongly simulated by one of several coherent state samplers. This allows us to study the resources needed for reaching a quantum computational advantage all on the level of the state. Understanding the hardness of boson sampling problems thus boils down to understanding for which quantum states it is computationally hard to sample from the Husimi Q-function. We use this approach to study the physical resources that are required to reach a quantum computational advantage with bosonic systems.
Techniques used: Non-Gaussian entanglement, coherent state sampling, stellar representation, phase space representations, Markov chain, …
