Research
In the multimode quantum optics group, we study the fundamental quantum properties and applications of light with many degrees of freedom (i.e. modes). Our activities are both theoretical and experimental, and the applications we consider range from quantum-inspired metrology and imaging, all the way to quantum information processing. We are mainly interested in the continuous-variable approach to light, which means that we rely on measurements of the electromagnetic field itself through homodyne detection.
Femtosecond Quantum Information
Multiplexing in time and frequency allows us to create large and versatile entangled states using quantum frequency combs. We use pulse shaping techniques to implement mode-selective measurements and operations (such as photon subtraction).
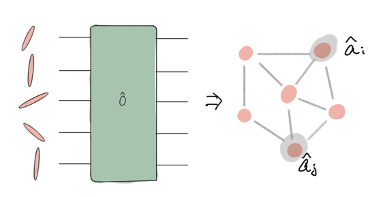
Quantum Complex Networks
Replicating complex networks in a scalable quantum platform is a formidable opportunity to learn more about the intrinsic quantumness of real world and for the efficient exploitation of quantum-complex structures in future technologies.
Quantum-inspired Metrology
Adapting many ideas and techniques from quantum optics to the field of imaging. We are specialised in the use of spatial-mode demultiplexing in such applications.
Theoretical Theory
Theoretical quantum optics and quantum information, with a strong focus on phase space representations and non-Gaussian effects.
News
Follow us on Bluesky!
More content coming soon.
The team
Team members
Discover who we areJobs
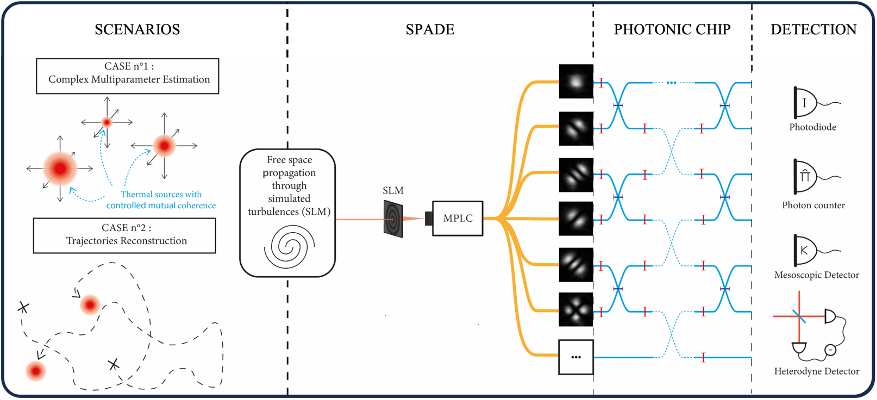
Post-doctoral position Modal approach to (quantum) multi-parameter estimation in optics
The Rayleigh criterion, once considered a fundamental limit in imaging, has been surpassed by quantum-inspired metrology techniques like Spatial Mode demultiplexing (SPADE) [1]. This post-doctoral project aims to extend SPADE’s capabilities to multi-parameter estimation, low-flux detection, and dynamic source tracking. The post-doc will work on/supervise an experimental setup aimed at multi-parameter estimation from individual incoherent optical sources [2] using a Multi-Plane Light Convertor [3]. She/He will also participate in the theoretical effort in deriving optimal quantum bounds [4] and optimal estimators [5].
The multimode quantum optics group pioneered the modal approach to quantum metrology [6] and obtained unparalleled sensitivity in source separation estimation [2] using a unique technology invented in the group [3]. The group has a strong experimental focus, but is also engaged in purely theoretical activities aiming at developing quantum optics in the continuous variable (CV) framework.
In a nutshell
Why to apply:
-you are passionate about fundamental quantum science and/or technological applications
-you will benefit from an international team of researchers who are experts in Continuous Variable quantum optics and metrology (theory and experiment)
– you will be in a group at the core of many national and international research networks
Our specific view:
– Experiments and theory should go together to implement practical parameter estimation at the quantum limit
– Modal approach to quantum metrology allows both for quantum limited parameter estimation and to derive theoretical bounds closely related
Environment
As a whole, the group has a tradition of working together with a diverse range of people from varied backgrounds. This diversity often leads to fruitful scientific input from different points of view, and it allows the group to explore new avenues. Furthermore, the moderate size of our group gives PhD students and postdocs the opportunity to discuss with PIs on a daily basis. This fosters a dynamic atmosphere with a lot of space for discussion.
Your work will be supported by the CEA-Audace project Lumiere, which aims to provide support and build collaborations. Notably, the project will enable you to gain access to groundbreaking multi-photon detectors with very high sensitivity and fast response time, promising significant advancements in metrology and tracking applications.
The project is inherently interdisciplinary, bridging quantum optics with fields such as signal processing, machine learning, and advanced instrumentation. It also benefits from strong collaborations with national and international teams, ensuring frequent exchanges of ideas and expertise.
Practical information
Candidates must hold an internationally recognized PhD in a field related to experimental quantum physics. A good background and past research track record in experimental optics, and quantum physics is required.
Application procedure: Inquiries and applications should be sent by email to Nicolas Treps(nicolas.treps@lkb.upmc.fr). Applications should include a detailed CV and two names of potential referees
Salary: Monthly net salary (after-tax) between 2200€ and 2900€, depending on experience
Application deadline: Preferentially apply before 16 May 2025
Starting date: flexible
Duration: 2 years (with possible renewal of 1 year)
References
[1] Tsang, M., Nair, R., & Lu, X. M. (2016). Quantum theory of superresolution for two incoherent optical point sources. Physical Review X, 6(3), 031033.
[2] Rouvière, C., Barral, D., Grateau, A., Karuseichyk, I., Sorelli, G., Walschaers, M., & Treps, N. (2024). Ultra-sensitive separation estimation of optical sources. Optica, 11(2), 166-170.
[3] G. Labroille, BertrDenolle, P. Jian, P. Genevaux, N. Treps, and J.-F. Morizur, Efficient and mode selective spatial mode multiplexer based on multi-plane light conversion, Opt Express 22, 15599 (2014).
[4] Gessner, M., Treps, N., & Fabre, C. (2023). Estimation of a parameter encoded in the modal structure of a light beam: a quantum theory. Optica, 10(8), 996-999.
[5] G. Sorelli, M. Gessner, M. Walschaers, and N. Treps, Optimal Observables and Estimators for Practical Superresolution Imaging, Phys. Rev. Lett. 127, 123604 (2021).
[6] C. Fabre and N. Treps, Modes and States in Quantum Optics, Rev. Mod. Phys. 92, 035005 (2020).
