Quantum-inspired Metrology

What is it all about?
Parameter estimation in the context of quantum metrology seeks to extract the maximum information from a quantum state about a specific parameter. Part of the group activity addresses the challenge of resolving incoherent light sources below the diffraction limit, with the key parameter to be estimated being the distance between two incoherent point sources. By utilizing suitable measurement techniques, such as spatial mode demultiplexing, one can overcome the Rayleigh limit and achieve superresolution, opening up new possibilities for surpassing the resolution constraints of conventional imaging methods.
M. Gessner, N. Treps, and C. Fabre, “Estimation of a parameter encoded in the modal structure of a light beam: a quantum theory,” Optica 10, 996-999 (2023)
Our approach: Spatial Mode Demultiplexing (SPADE)
Direct imaging (DI) can be understood as decomposing light onto a pixel basis. However, by measuring only local intensity, one loses the phase information intrinsic to the light field. A more informative strategy for distance estimation is to demultiplex the light in a different orthogonal but delocalized basis—specifically, the spatial Hermite-Gauss modes. This allows us to recover spatial correlations and significantly enhance the amount of information accessible about the distance between the sources.
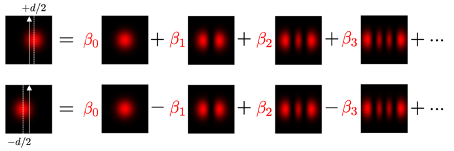
G. Sorelli, M. Gessner, M. Walschaers, N. Treps, “Optimal observables and estimators for practical superresolution imaging” Phys. Rev. Lett. 127, 123604 (2021).
Multiplane Light Converter: A Journey from Research to Industry and Back
To experimentally realize SPADE, we rely on a device first developed over a decade ago by the Multimode Quantum Optics group: the Multiplane Light Converter. This innovation not only laid the foundation for cutting-edge laboratory work but also gave rise to Cailabs, a company enhancing fiber and satellite communication through advanced demultiplexing techniques. After years of dedicated engineering in an industrial setting, the demultiplexer returns to the lab with exceptional performance—offering large numbers of modes, high mode selectivity, remarkable reproducibility, and minimal losses.

G. Labroille, B. Denolle, P. Jian, P. Genevaux, N. Treps, and J.-F. Morizur, “Efficient and mode selective spatial mode multiplexer based on multi-plane light conversion,” Opt. Express 22, 15599-15607 (2014)
Single parameter estimation
In the case of equally bright sources, the demultiplexer can be conveniently aligned so that its origin matches the centroid of the scene—that is, the geometric midpoint between the sources. In this configuration, where all crucial parameters are known except for the separation distance, we achieve distance estimation with a sensitivity five orders of magnitude below the diffraction limit. These results challenge the Rayleigh criterion, effectively rendering it obsolete for passive imaging.
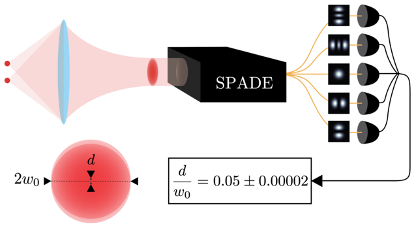
C. Rouvière, D. Barral, A. Grateau, I. Karuseichyk, G. Sorelli, M. Walschaers, and N. Treps, “Ultra-sensitive separation estimation of optical sources”Optica 11, 166-170 (2024).
Multiparameter approach
In most of real case scenarios, one has to deal with unequally bright sources. And because centroid alignment becomes none trivial, the scene is now characterized by 3 unknown parameters: the distance, the brightness imbalance and the misalignment. By optimizing the measurement basis and applying advanced machine learning estimation strategies, we aim to measure separations beyond the diffraction limit also in this context. While still in progress, our approach holds promise for advancing optical resolution, with impactful applications in high-resolution imaging, microscopy, and astronomy.

